Half-Life Calculator
Half-Life Calculator
Use this calculator to calculate the half-life, remaining quantity, decay constant, or mean lifetime of a substance based on the time passed.
Results:
Remaining Quantity (Nt): - kg
Decay Constant (λ): - 1/s
Mean Lifetime (τ): - seconds
Understanding the concept of half-life is crucial in various fields such as chemistry, physics, biology, and even medicine. Whether you’re studying radioactive decay, drug metabolism, or carbon dating, being able to estimate half-life accurately can help you make better predictions and decisions. A half-life calculator is a tool that simplifies this complex calculation, making it accessible and easy to use for both students and professionals.
In this article, we’ll explore how a half-life calculator works, how to use it effectively, and why it’s an essential tool for your academic or professional toolkit.
What Is a Half-Life?
Before diving into the details of the half-life calculator, let’s briefly define half-life.
Half-life refers to the time it takes for half of a substance to decay or transform into another form. This concept is most commonly associated with radioactive elements, but it also applies to substances like drugs in the body and even certain chemical reactions. The half-life is a critical factor in many scientific calculations and predictions.
How Does a Half-Life Calculator Work?
A half-life calculator uses the classic formula for radioactive decay or exponential decay:
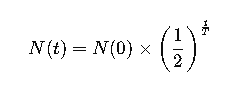
Where:
- N(t) = the remaining quantity of the substance after time t
- N(0) = the initial quantity of the substance
- T = the half-life time of the substance
- t = the total time elapsed
Estimate Half-Life with Precision
Using a half-life calculator online is a quick and reliable way to estimate half-life, whether you’re working with substances like uranium, carbon-14, or even medications. The calculator takes into account the initial quantity, half-life time, and total time elapsed, giving you the precise remaining amount of the substance.
Key Features of a Half-Life Calculator
A good half-life calculator will have these essential features:
- User-friendly interface: You simply input the initial amount, half-life time, and elapsed time.
- Accurate results: It calculates the remaining quantity using the correct formula.
- Additional tools: Some calculators allow you to estimate other related values like the decay constant (λ) or the mean lifetime (τ).
- Graphical representation: Many tools offer a visual graph showing the decay over time, making the results easier to understand.
How to Use a Half-Life Calculator?
Let’s walk through the process of using a half-life calculator:
- Input Initial Quantity: Enter the initial amount of the substance (e.g., 100 grams of a radioactive element).
- Enter Half-Life Time: Provide the half-life time of the substance (e.g., 20 years).
- Provide Elapsed Time: Input the total time that has passed (e.g., 60 years).
- Click Calculate: Press the “Calculate” button to get the remaining quantity.
- View Results: The calculator will display the remaining amount, along with optional values like decay constant (λ) or mean lifetime (τ).
Example: Calculate Half-Life for Radioactive Decay
Let’s say you have 100 grams of a substance with a half-life of 20 years, and 60 years have passed. Using the half-life calculator:

The calculator will instantly tell you that after 60 years, only 12.5 grams of the original 100 grams remains.
Why You Need a Half-Life Calculator Online
Half-life calculators online are indispensable for students, scientists, and anyone involved in fields that require precise decay calculations. Here’s why:
- Quick results: No need to manually perform complex calculations.
- Accurate and reliable: Online tools are based on proven mathematical formulas.
- Accessible anytime, anywhere: You can calculate half-life from any device with an internet connection.
- Great for educational purposes: Teachers and students can use it to demonstrate the concept of radioactive decay and other scientific principles.
Additional Tips for Using a Half-Life Calculator
Here are some tips to get the most out of your half-life calculator:
- Double-check units: Ensure all units (e.g., grams, years, seconds) are consistent before performing calculations.
- Understand exponential decay: Remember, the decay process follows an exponential curve, meaning the substance won’t lose half its quantity in the same time intervals if the time is not a multiple of the half-life.
- Use the graph feature: Many calculators offer graphs that show how the substance decays over time. This can help you visualize the decay process more effectively.
- Estimate multiple values: Some calculators allow you to compute other variables like decay constant (λ) or mean lifetime (τ) for a more complete analysis.
In conclusion, a half-life calculator is an essential tool for anyone dealing with exponential decay processes, whether in scientific research, education, or daily life. By understanding how to use it effectively, you can streamline calculations and gain valuable insights into the behavior of substances over time.
Share this article with friends or colleagues who may benefit from it, and subscribe to our newsletter for more useful tools and resources.
FAQs
1. What is the half-life formula?
The half-life formula is used to calculate the remaining quantity of a substance after a specific amount of time:
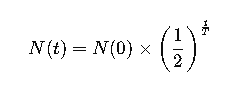
Where T is the half-life, t is the time elapsed, and N(0) is the initial quantity.
2. How do I estimate half-life?
To estimate half-life, you can use the half-life calculator online by inputting the initial quantity, total time elapsed, and the substance’s half-life. The tool will calculate the remaining quantity and give you an estimation of the decay over time.
3. Can I use a half-life calculator for biological decay?
Yes, you can use the half-life calculator to estimate the decay of substances in biological systems, such as drugs or metabolites in the human body. The same principles of exponential decay apply.
4. How accurate are online half-life calculators?
Online half-life calculators are highly accurate as long as you input the correct values for the initial quantity, half-life time, and elapsed time. These calculators rely on well-established mathematical formulas.
